Prices of a Future contract and a Forward contract are the same under the Black-Scholes assumptions (deterministic rates) but the price of options on Futures or options on Forwards might still differ. I did not find this obvious at first.
For example, when the underlying contract expiration date (Futures, Forward) is different from the option expiration date. For a Future Option, the Black-76 formula can be used, the discounting is done from the option expiry date, because one receives the cash on expiration due to the margin account. For a Forward Option, the discounting need to be done from the Forward contract expiry date.
European options prices will be the same when the underlying contract expiration date is the same as the option expiration date. However, this is not true for American options: the immediate exercise will need to be discounted to the Forward expiration date for a Forward underlying, not for a Future.
Thursday, November 21, 2013
American Option on Forward/Futures
Prices of a Future contract and a Forward contract are the same under the Black-Scholes assumptions (deterministic rates) but the price of options on Futures or options on Forwards might still differ. I did not find this obvious at first.
For example, when the underlying contract expiration date (Futures, Forward) is different from the option expiration date. For a Future Option, the Black-76 formula can be used, the discounting is done from the option expiry date, because one receives the cash on expiration due to the margin account. For a Forward Option, the discounting need to be done from the Forward contract expiry date.
European options prices will be the same when the underlying contract expiration date is the same as the option expiration date. However, this is not true for American options: the immediate exercise will need to be discounted to the Forward expiration date for a Forward underlying, not for a Future.
For example, when the underlying contract expiration date (Futures, Forward) is different from the option expiration date. For a Future Option, the Black-76 formula can be used, the discounting is done from the option expiry date, because one receives the cash on expiration due to the margin account. For a Forward Option, the discounting need to be done from the Forward contract expiry date.
European options prices will be the same when the underlying contract expiration date is the same as the option expiration date. However, this is not true for American options: the immediate exercise will need to be discounted to the Forward expiration date for a Forward underlying, not for a Future.
Wednesday, November 20, 2013
Spikes in Heston/Schobel-Zhu Local Volatility
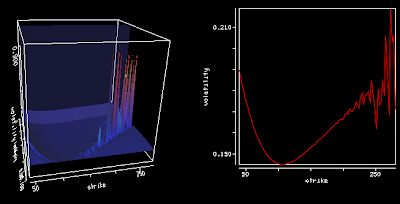
Using precise vanilla option pricing engine for Heston or Schobel-Zhu, like the Cos method with enough points and a large enough truncation can still lead to spikes in the Dupire local volatility (using the variance based formula).
The large spikes in the local volatility 3d surface are due to constant extrapolation, but there are spikes even way before the extrapolation takes place at longer maturities. Even if the Cos method is precise, it seems to be not enough, especially for large strikes so that the second derivative over the strike combined with the first derivative over time can strongly oscillate.
After wondering about possible solutions (using a spline on the implied volatilities), the root of the error was much simpler: I used a too small difference to compute the numerical derivatives (1E-6). Moving to 1E-4 was enough to restore a smooth local volatility surface.
 |
| Local Volatility |
 |
| Implied Volatility |
The large spikes in the local volatility 3d surface are due to constant extrapolation, but there are spikes even way before the extrapolation takes place at longer maturities. Even if the Cos method is precise, it seems to be not enough, especially for large strikes so that the second derivative over the strike combined with the first derivative over time can strongly oscillate.
After wondering about possible solutions (using a spline on the implied volatilities), the root of the error was much simpler: I used a too small difference to compute the numerical derivatives (1E-6). Moving to 1E-4 was enough to restore a smooth local volatility surface.
Spikes in Heston/Schobel-Zhu Local Volatility
Using precise vanilla option pricing engine for Heston or Schobel-Zhu, like the Cos method with enough points and a large enough truncation can still lead to spikes in the Dupire local volatility (using the variance based formula).
The large spikes in the local volatility 3d surface are due to constant extrapolation, but there are spikes even way before the extrapolation takes place at longer maturities. Even if the Cos method is precise, it seems to be not enough, especially for large strikes so that the second derivative over the strike combined with the first derivative over time can strongly oscillate.
After wondering about possible solutions (using a spline on the implied volatilities), the root of the error was much simpler: I used a too small difference to compute the numerical derivatives (1E-6). Moving to 1E-4 was enough to restore a smooth local volatility surface.
 |
| Local Volatility |
 |
| Implied Volatility |
The large spikes in the local volatility 3d surface are due to constant extrapolation, but there are spikes even way before the extrapolation takes place at longer maturities. Even if the Cos method is precise, it seems to be not enough, especially for large strikes so that the second derivative over the strike combined with the first derivative over time can strongly oscillate.
After wondering about possible solutions (using a spline on the implied volatilities), the root of the error was much simpler: I used a too small difference to compute the numerical derivatives (1E-6). Moving to 1E-4 was enough to restore a smooth local volatility surface.
Subscribe to:
Comments
(
Atom
)
